証明
$h$の存在を示す。

$g$は$f \circ g = 0$を満たすから、任意の$x \in N$に対して

$$f\qty\big(g(x)) = 0$$

「線形写像の合成と包含関係」より、

$$\iff g(x) \in \ker f.$$

よって、このような$g$とに対して、$g(x) = h(x)$とすることで、$g$は$R$-線形写像になるから、$h$も$R$-線形写像になる。

$\iota \circ h = g$が成り立つことを示す。

$$= (\iota \circ h)(x)$$

$$= \iota\qty\big(h(x))$$

$\iota$は包含写像であるから、

$$= h(x)$$

$h$の定義より、$h(x) = g(x)$であるから、

$$= g(x).$$

となり、$\iota \circ h = g$が得られる。

$h$の一意性を示す。

$\iota \circ h’ = g$を満たす写像$h’ \colon N \to \ker f$が存在するとすると、

$$\iota\qty\big(h(x)) = \iota\qty\big(h'(x))$$

「包含写像は単射」より、$\iota$は単射であるから、

$$\implies h(x) = h'(x)$$

よって、$h = h’$となり、$h$は一意的に存在する。$\Box$

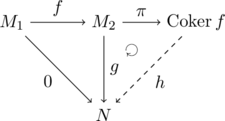
証明
$h$の存在を示す。

$\pi$は全射であるから、任意の$x + \im f \in \coker f$に対して、$\pi(x) = y$となる$y \in M_2$が存在する。

$x + \im f = x’ + \im f$とすると、

$$x + \im f = x’ + \im f$$

$$\iff x – x’ \in \im f$$

ある$y \in M_1$が存在して、

$$\iff x – x’ = f(y)$$

$$\iff x = x’ + f(y)$$

と表せる。

$$g(x) = g\qty\big( x’ + f(y) )$$

$g$は$R$-線形写像であるから、

$$= g(x’) + g\qty\big( f(y) )$$

$$= g(x’) + (g \circ f)(y)$$

仮定より、$g \circ f = 0$が成り立つから、

$$= g(x’)$$

が得られる。$h(x + \im f) = h(x’ + \im f)$であるから、$h(x + \im f) = g(x)$と定めることができ、$g$は$R$-線形写像であるから、$h$も$R$-線形写像になる。

$h \circ \pi = g$が成り立つことを示す。

$$(h \circ \pi)(x) = h\qty\big( \pi(x) )$$

$$= h( x + \im f )$$

$$= g(x)$$

となる。よって、$h \circ \pi = g$が成り立つ。

$h$の一意性を証明する。

$h \circ \pi = g$を満たす写像$h’ \colon \coker f \to N$が存在するとすると、

$$h( x + \im f)$$

$$= h\qty\big( \pi(x) )$$

$g = h \circ \pi,\, g = h’ \circ \pi$より$h \circ \pi = h’ \circ \pi$が成り立つから、

$$= h’\qty\big( \pi(x) )$$

$$= h'( x + \im f)$$

よって、$h = h’$となり、$h$は一意的に存在する。