環上の加群の直和とその普遍性

$R$-加群の直和を導入するために、まずは$R$-加群の直積を定義する。

定義1: $R$-加群の直積ちょくせき

命題1: $R$-加群の直積の$R$-加群$\dprod_{i \in I} M_i$を$R$-加群の直積ちょくせきと呼ぶ。

命題1: $R$-加群の直積

$R$を環、$M_i \ (i \in I)$を$R$-加群とし、集合としての直積の元$(x_i)_{i \in I}, (y_i)_{i \in I} \in \dprod_{i \in I} M_i$に以下の演算を定義するとき、$\dprod_{i \in I} M_i$は$R$-加群をなす。

$(x_i)_{i \in I} + (y_i)_{i \in I} = (x_i + y_i)_{i \in I}$
$a(x_i)_{i \in I} = (ax_i)_{i \in I}$

右分配律の証明

$a\qty\big( (x_i)_{i \in I} + (y_i)_{i \in I} )$

$= a(x_i + y_i)_{i \in I}$

$= \qty\big( a(x_i + y_i) )_{i \in I}$

$= \qty\big( (ax_i + ay_i) )_{i \in I}$

$= (ax_i)_{i \in I} + (ay_i)_{i \in I}$

$= a(x_i)_{i \in I} + a(y_i)_{i \in I}.$

左分配律の証明

$(a + b)(x_i)_{i \in I}$

$= \qty\big( (a + b)x_i )_{i \in I}$

$= \qty\big( (ax_i + bx_i) )_{i \in I}$

$= (ax_i)_{i \in I} + (bx_i)_{i \in I}$

$= a(x_i)_{i \in I} + b(x_i)_{i \in I}.$

結合律の証明

$(ab)(x_i)_{i \in I}$

$= (abx_i)_{i \in I}$

$= \qty\big( a(bx_i) )_{i \in I}$

$= a(bx_i)_{i \in I}$

$= a\qty\big( b(x_i)_{i \in I} ).$

単位律の証明

$1_R (x_i)_{i \in I}$

$= (1_R x_i)_{i \in I}$

$= (x_i)_{i \in I}. \Box$

集合としての直積$M_1 \times M_2$と、$R$-加群としての直積$M_1 \times M_2$の表記を区別することはない。
区別せずとも不利益が生ずることがなく、集合としての直積を扱う機会が少ないからである。

定義2: $R$-加群の直和ちょくわ

$R$を環、$M_i \ (i \in I)$を$R$-加群とするとき、$\dbigoplus_{i \in I} M_i := \left\{ (x_i)_{i \in I} \in \dprod_{i \in I} M_i \,\right|\,有限個の$$\left.i \in I を除いてx_i = 0_R\rule{0pt}{4ex}\right\}$を$R$-加群の直和ちょくわと呼ぶ。

定理1: $R$-加群の直和の普遍性

$R$を環、$M_1,\, M_2$を$R$-加群、$\iota, f_i$を$R$-線形写像とするとき、以下のように$f \circ \iota_i = f_i$が成り立ち、図式を可換にする$R$-線形写像$f \colon \dbigoplus_{i \in I} M_i \to M’$がただ一つ存在する。

Rendered by QuickLaTeX.com

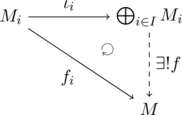
$f$が存在すること、$R$-線形写像であること、存在が一意的であることを順に示していく。

$f$ の存在の証明
$\dbigoplus_{i \in I} M_i$において、有限個の$i_\lambda \in I \ (1 \leq \lambda \leq n)$を除いて$x_i = 0$であるとするとき、$\iota_i$を$\iota_i \colon x \mapsto (x_i)_{i \in I}$、$f$を$f \colon (x_i)_{i \in I} \mapsto \dsum_{i \in I} f_i(x_i)$と定義すると、

$x \in M_i$に対して、

$f\qty\big( \iota_i(x) )$

$= f\qty\big( (x_i)_{i \in I} )$

$= \dsum_{i \in I} f_i(x_i)$

有限個の $x_i \neq 0$ の部分と、それ以外の $x_i = 0$ の部分に分けられるから、

$= \dsum_{i = 1}^n f_{i_\lambda}(x_{i_\lambda}) + \dsum_{\substack{i \neq i_\lambda i \in I}} f_i(0)$

「群準同型写像の性質」より、

$= \dsum_{i = 1}^n f_{i_\lambda}(x_{i_\lambda})$

となる。よって、$f \circ \iota_i = f_i$が成り立つような$f$は存在する。$\Box$

$f$が$R$-線形写像であることの証明
加法性：

$f\qty\big( \iota_i(x + y) )$

$= f\qty\big( (x_i)_{i \in I} + (y_i)_{i \in I} )$

$= f\qty\big( (x_i + y_i)_{i \in I} )$

$= \sum_{i = 1}^n f_i(x_i + y_i)$

$f_i$ は$R$-線形写像であるから、

$= \sum_{i = 1}^n f_i(x_i) + f_i(y_i)$

$= \sum_{i = 1}^n f_i(x_i) + \sum_{i = 1}^n f_i(y_i)$

$= f\qty\big( (x_i)_{i \in I} ) + f\qty\big( (y_i)_{i \in I} )$

$= f\qty\big( \iota_i(x) ) + f\qty\big( \iota_i(y) ).$

斉次性：

$f\qty\big( \iota_i(ax) )$

$= \dsum_{i = 1}^n f_i(ax_i)$

$f_i$ は $R$-線形写像であるから、

$= \dsum_{i = 1}^n af_i(x_i)$

$= a\dsum_{i = 1}^n f_i(x_i)$

$= af\qty\big( \iota_i(x) ).\Box$

$f$の一意性の証明
$f$と同じ役割を果たす$R$-線形写像$g \colon \dbigoplus_{i \in I} M_i \to M;\, (x_i)_{i \in I} \mapsto \dsum_{i \in I} f_i(x_i)$を定義すると、

$g\qty\big( (x_i)_{i \in I} )$

$= \sum_{i \in I} f_i(x_i)$

$= f\qty\big((x_i)_{i \in I})$

よって、$g = f$となり、$f$は一意的に存在する。$\Box$

$R$-加群の直和は普遍性を満たすことがわかったが、圏論的には、$R$-加群の直積は$R$-加群の圏$\Mod{R}$における積せき、$R$-加群の直和は$\Mod{R}$における余積よせきに対応し、それぞれ普遍性によって定義される。
つまり、圏論的な視点によると、$R$-加群の直和は$R$-加群の直積の双対概念である。
可換環論における直和の定義の仕方は「有限個を除いて$0$」と気持ち悪いかもしれないが、圏論的に俯瞰して見ると、直積と双対になっているわけである。
もちろん、直和が自由加群であり、その有限性を用いると扱いやすいという側面もある。