加群のテンソル積【普遍性と一意性】

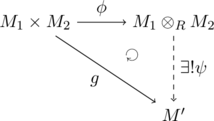
証明

直和$\dbigoplus_{(x, y) \in M_1 \times M_2} R(x, y)$を定義すると、これは$M_1 \times M_2$を基底とする自由加群であることがわかり、各元は$\dbigoplus_{(x, y) \in M_1 \times M_2} R(x, y) = \dsum_{i = 1}^n a_i(x_i, y_i)$という形で表せる。

$\dbigoplus_{(x, y) \in M_1 \times M_2} R(x, y)$の部分集合
\begin{align*}
S_1 & = \qty\Big{ (x_1 + x_2, y) – (x_1, y) – (x_2, y) \Bigm x_1, x_2 \in M_1, y \in M_2 }, \\
S_2 & = \qty\Big{ (x, y_1 + y_2) – (x, y_1) – (x, y_2) \Bigm x \in M_1, y_1, y_2 \in M_2, a \in R }, \\
S_3 & = \qty\big{ (ax, y) – a(x, y) \bigm x \in M_1, y \in M_2, a \in R }, \\
S_4 & = \qty\big{ (x, ay) – a(x, y) \bigm x \in M_1, y \in M_2, a \in R }
\end{align*}

を定義し、これらが生成する部分$R$-加群を$\langle S\rangle := \langle S_1 \cup S_2 \cup S_3 \cup S_4\rangle $とする。

$\phi \colon M_1 \times M_2 \to \dfrac{ \dbigoplus_{(x, y) \in M_1 \times M_2} R(x, y) }{\langle S\rangle };\, (x, y) \mapsto (x, y) + \langle S\rangle $が$R$-双線形写像であることを示す。

\begin{align*}
\phi(x_1 + x_2, y)
& = (x_1 + x_2, y) + \langle S\rangle \\
(x_1 + x_2, y) – (x_1, y) – (x_2, y) \in \langle S\rangle より、\alignfootnote{\alpha + \beta \in \langle S\rangle \iff \qty\big( \alpha + \langle S\rangle ) = \qty\big( \beta + \langle S\rangle )を用いている。
& = \qty\big( (x_1, y) + (x_2, y) ) + \langle S\rangle \\
& = \qty\big( (x_1, y) + \langle S\rangle ) + \qty\big( (x_2, y) + \langle S\rangle ) \\
& = \phi(x_1, y) + \phi(x_2, y). \\[2ex]
%
\phi(x, y_1 + y_2)
& = (x, y_1 + y_2) + \langle S\rangle \\
(x, y_1 + y_2) – (x, y_1) – (x, y_2) \in \langle S\rangle より、
& = \qty\big( (x, y_1) + (x, y_2) ) + \langle S\rangle \\
& = \phi( (x, y_1) + (x, y_2) ). \\[2ex]
%
\phi(ax, y)
& = (ax, y) + \langle S\rangle \\
(ax, y) – a(x, y) \in \langle S\rangle より、
& = a(x, y) + \langle S\rangle \\
& = a\phi(x, y). \\[2ex]
%
\phi(x, ay)
& = (x, ay) + \langle S\rangle \\
(x, ay) – a(x, y) \in \langle S\rangle より、
& = a(x, y) + \langle S\rangle \\
& = a\phi(x, y).
\end{align*}

となるから、$\phi$は$R$-双線形写像である。

$x’ \in M’$とすると、「R-加群の直和の普遍性」より、$R$-線形写像$g’ \colon \dbigoplus_{(x, y) \in M_1 \times M_2} R(x, y) \to M’$がただ一つ存在する。

\begin{align*}
g’\qty\big( (x_1 + x_2, y) – (x_1, y) – (x_2, y) )
& = g'(x_1 + x_2, y) – g'(x_1, y) – g'(x_2, y)
g’はR-線形写像であるから、
& = g(x_1 + x_2, y) – g(x_1, y) – g(x_2, y)
gはR-双線形写像であるから、
& = g(x_1 + x_2 – x_1 – x_2, y – y) \\
& = g(0, 0)
「群準同型写像の性質(i)」より、
& = 0. \\[2ex]
g’\qty\big( (x, y_1 + y_2) – (x, y_1) – (x, y_2) )
& = g'(x, y_1 + y_2) – g'(x, y_1) – g'(x, y_2) \\
& = g(x, y_1 + y_2) – g(x, y_1) – g(x, y_2) \\
& = g(x – x, y_1 + y_2 – y_1 – y_2) \\
& = g(0, 0) \\
& = 0. \\[2ex]
g’\qty\big( (ax, y) – a(x, y) )
& = g'(ax, y) – g’\qty\big( a(x, y) ) \\
& = g(ax, y) – g\qty\big( a(x, y) ) \\
& = g(ax, y) – g(ax, y) \\
& = g(ax – ax, y – y) \\
& = g(0, 0) \\
& = 0. \\[2ex]
g’\qty\big( (x, ay) – a(x, y) )
& = g'(x, ay) – g’\qty\big( a(x, y) ) \\
& = g(x, ay) – g\qty\big( a(x, y) ) \\
& = g(x, ay) – g(x, ay) \\
& = g(x – x, ay – ay) \\
& = g(0, 0) \\
& = 0.
\end{align*}
となる。よって、
\begin{align*}
& g’\qty\big( \langle S\rangle ) = \qty{0} \\
\iff & \langle S\rangle \subseteq \ker g’
\end{align*}

となる。

以下のような図式を考えると、

「加群準同型定理」より、$g’ = \psi \circ \phi$となる$R$-線形写像$\psi \colon \dfrac{ \dbigoplus_{(x, y) \in M_1 \times M_2} R(x, y) }{\langle S\rangle } \to M’$がただ一つ存在する。
したがって、$g = \psi \circ \phi$が成り立つ$\psi$がただ一つ存在することが分かった。\Box

証明

$T_1, T_2$に対して、テンソル積の定義より、以下の図式が成り立つ。

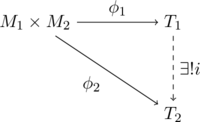
この関係をまとめて、以下のような図式に書き換える。

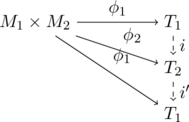
真ん中の$T_2, T_1$を消して、

上の図式より、

\begin{align*}
& \phi_1 = (i’ \circ i) \circ \phi_1, \phi_2 = (i \circ i’) \circ \phi_2 \\
\implies & i’ \circ i = \id_{T_1}, i \circ i’ = \id_{T_2}
\end{align*}

が導かれる。以上より$i’$は$i$の逆写像であるから、「逆写像の存在と全単射」より、$i$は全単射であり、かつ$i$は$R$-線形写像と定義したから、$i \colon T_1 \to T_2$は$R$-同型写像である。\Box